 The solar system embedded in a graph network.
The solar system embedded in a graph network.
Rediscovering orbital mechanics with machine learning
Paper authors: Pablo Lemos, Niall Jeffrey, Miles Cranmer, Shirley Ho, Peter Battaglia
If machine learning were around in the 1600s, would Newton have discovered his law of gravitation?
\[\mathbf{F} = -\frac{G M m}{r^2}\hat{r}\]Or, would scientists have relied on black box regression models to make their predictions, and missed the simple rules underlying nature?
In our paper, we ask the fundamental question:
Could an algorithm discover the law of universal gravitation?
It is one challenge to take a known model and infer the parameters in a system described by the model. It is another to take a system with known parameters and infer the rules underlying the system.
Here, we ask for both. Can we infer both the model and the parameters, simultaneously?
Machine learning has the potential to accelerate all facets of discovery in the natural sciences, if used with care. When we use machine learning in science as a black box regression model, without interest in how the trained model is actually making a prediction, we miss a fundamental part of of the process. Science is about understanding the world around us, and so to use machine learning for actual insight, we must understand the trained model.
In our paper, now available on arXiv, we demonstrate that it is possible to discover not only the rules which describe a system, but also to do so without knowing the actual parameters needed by those rules.
This “automated discovery” algorithm we propose contains two separate parts, largely based on the framework given in Cranmer et al., 2020: first, we train a neural network to model the dynamics of a system. Second, we distill this neural network into a simple symbolic rule using symbolic regression (with PySR).
However, unlike Cranmer+2020, here the physical parameters in the system are missing: things like mass, charge, or other physical properties. These must be inferred simultaneously with the law! To do so, we initialize trainable variables representing such parameters, and optimize these variables along with the model’s parameters using a single optimizer.
Data
Many works in symbolic regression (including some of our own) have historically focused on toy simulations. This misses out on the messiness of the real world: noise, missing information, large dynamic ranges, unknown physical constants, etc. Here, we will rediscover orbital mechanics directly from observations of the solar system.
We develop a training dataset based on “ephemeris” data from NASA’s Horizons, selecting the 31 bodies in our solar system with masses above kg: the sun, the planets, Pluto, and a selection of moons. Our training portion is the positions of these bodies at 30-minute intervals for a 30 year period from 1980 to 2010, and a validation set using 2010-2013.
Model
Our learned model is a Graph Neural Network (GNN) based on the “Interaction Network” defined in Battaglia et al., 2018, with learned node attributes and one message passing step. GNNs are well-suited for physical datasets: they treat interactions between objects (represented as nodes) explicitly via message passing, and allow one to easily embed symmetries such as permutation, translation, and rotational equivariances into the network.
The only input to our GNN are the positions and velocities of the body at a given moment in time, as well as a learned parameter for each body. From training the GNN to predict the acceleration of each body, we can learn a force that models the dynamics of the system, as well as the masses of the bodies. Exact training details are given in the paper.
After training, we can study the performance of the model in the years 2010-2013, using the validation set:
The performance of this pure GNN is okay, but not great, at predicting the dynamics of this system. The prediction errors quickly accumulate over long rollouts. Next, let’s see if we can interpret the internal rules learned by this model using the framework of Cranmer et al., 2020.
Distilling symbolic rules
We next wish to discover what rules the GNN has actually learned to predict these dynamics. In doing so, we hope to recover a scientific insight: in this case, rediscovering Newton’s law of gravity. Compressing our model to a set of symbolic rules may also help us with improved generalization (especially in this case if it recovers the true law!).
To do this, we fit the inputs and outputs of our GNN’s message-passing module using symbolic regression, a machine learning algorithm that searches through millions symbolic expressions to fit data. We use the PySR algorithm (Cranmer, 2022) for this task, which uses a type of evolutionary algorithm.
We recover the following expressions:

More complex expressions more accurate at approximating the GNN’s internal function. However, one can always add terms to a simple expression to improve its accuracy, so simplicity and accuracy much be balanced. We use the same score as in Cranmer et al., 2020, and this successfully recovers Newton’s law of gravity (shown in teal blue).
We can then take this recovered law, and put it back into the message-passing module of our GNN. Let’s see how this performs compared to the earlier model:
The performance certainly looks better! However, it is still not perfect. Why is that?
To solve this issue, let’s look at the learned parameters for each body in comparison to the true masses (normalized to the sun’s mass):
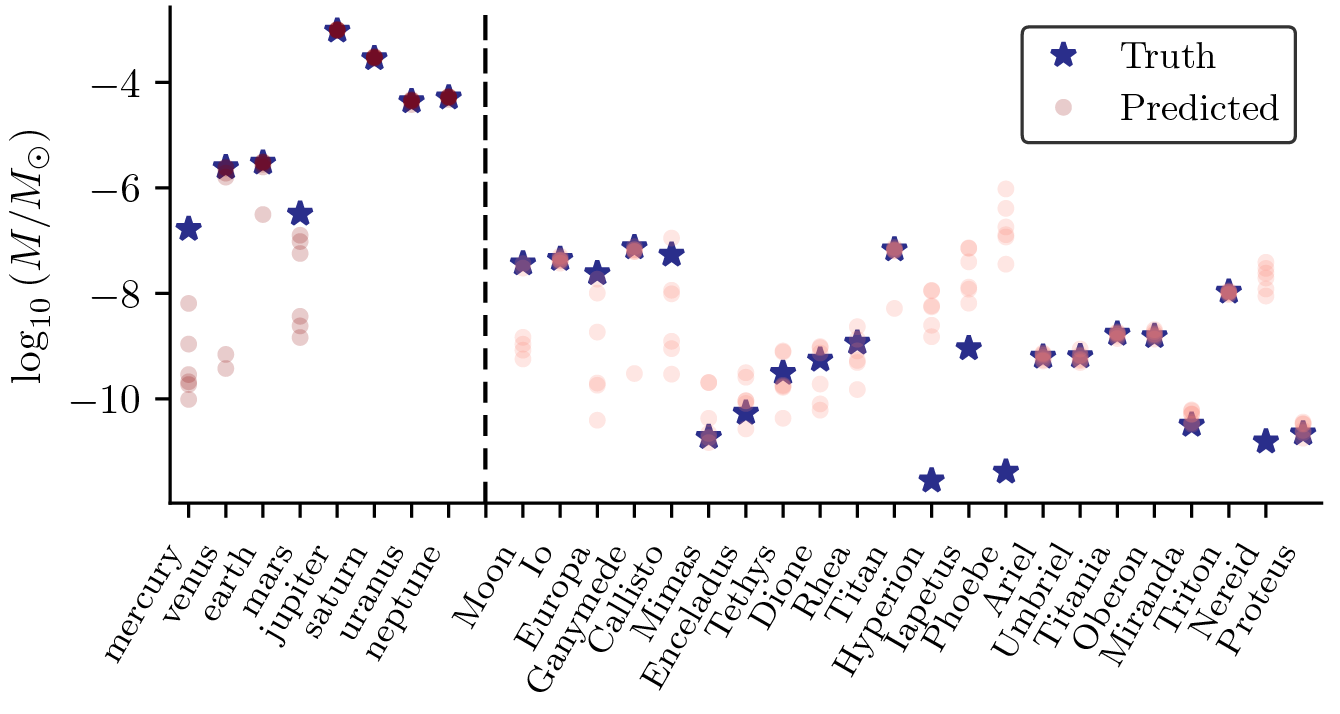
Many of these mass parameters are quite off-the-mark compared to the true masses for each body! Even many of the planets, which should have a large gravitational effect on other planets, are sometimes orders of magnitude off from the ground truth.
At this point in our project we had a realization about our approach. While Newton’s law of gravity is a fairly good approximation of the message-passing function in the GNN, it is not an exact fit. Neural Networks can learn highly nonlinear functions and demonstrate very unexpected behaviour. Therefore, while these mass parameters may be very good inputs to the GNN, they may not be the best inputs to the symbolic version of the GNN!
Thus, we decided to re-fit the mass parameters through this fixed symbolic expression. This produced a much better rollout:
In addition, this also gave us mass estimates which are must closer to the ground truth!
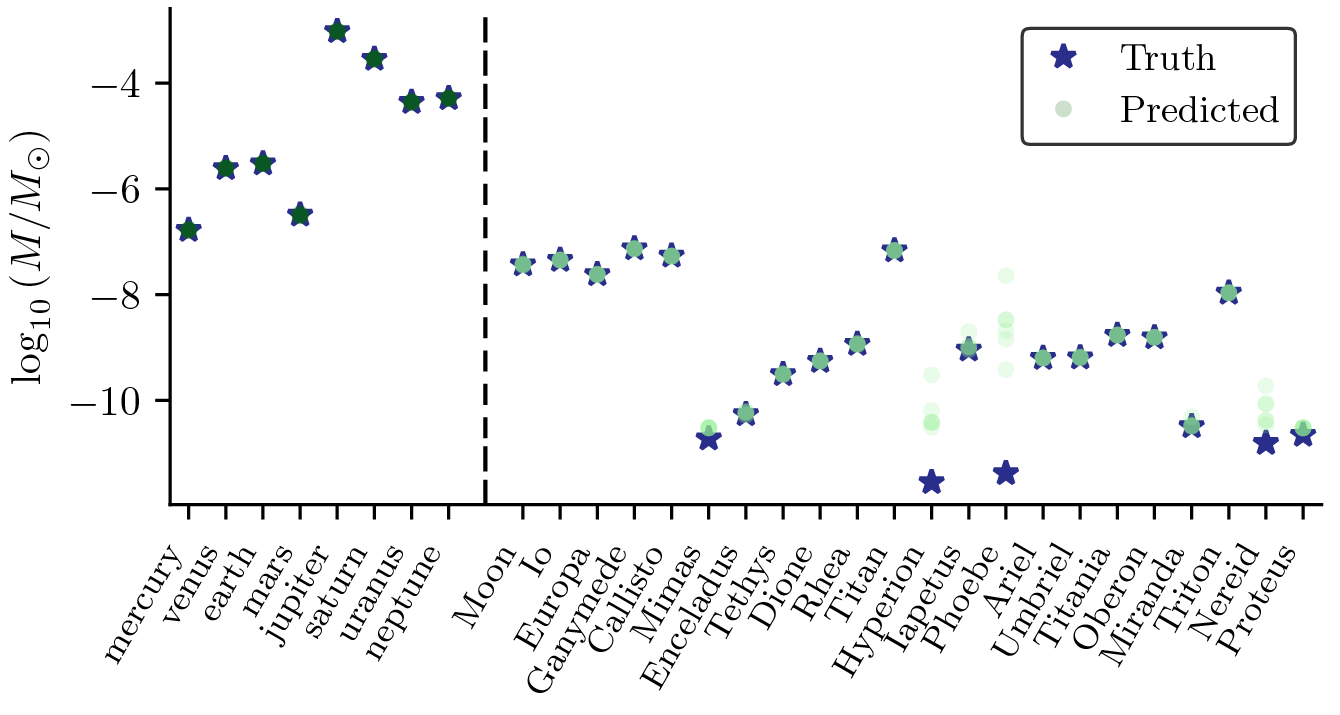
When we do this, we obtain masses which almost perfectly match the true ones. Why almost? Far from being a problem, this turns out to be proof that the algorithm is working: According to the equivalence principle, a bodies’ mass only affects the trajectories of other bodies. In other words, if the Earth was twice the size, the trajectory of the Moon would be greatly affected, but Earth’s trajectory around the Sun would remain the same. In the case of bodies like Phoebe, Hyperion and Nereid, we notice that they are very small moons, which have negligible influence in the trajectories of other bodies. Therefore, their masses do not affect the system in any way, as long as it remains small! To confirm this theory, we estimated the gravitational influence that each body has on the rest, and plotted it against the error in the mass estimate.
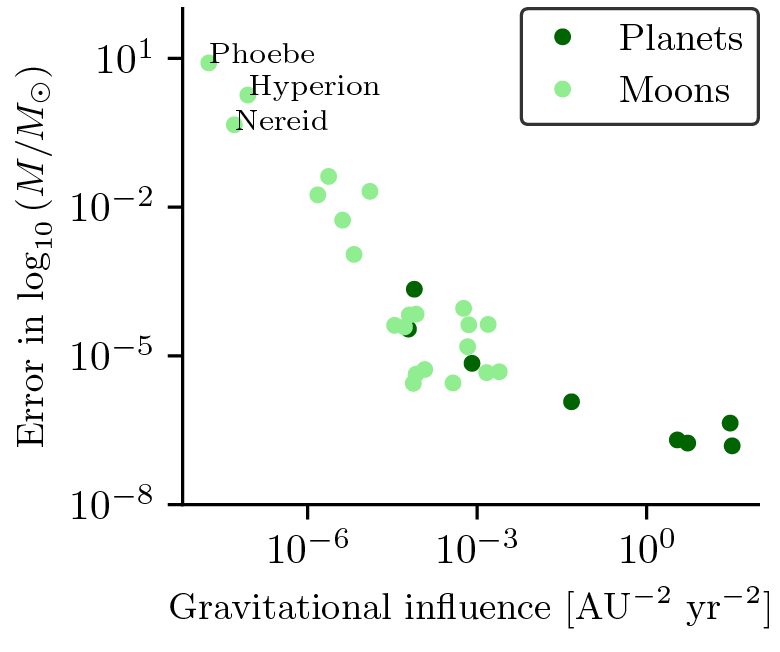
And we found on the right side of the above plot, indeed, a clear anti-correlation between the two, meaning that the less a body influences the rest, the worst our mass estimate is!
Therefore, we can see how how our algorithm has successfully learned the correct force law, and the masses of the bodies, simultaneously!